Wozu werden Planetengetriebe verwendet?

PlanetengetriebePlanetengetriebe, auch bekannt als Planetengetriebe, werden aufgrund ihrer kompakten Bauweise, ihres hohen Wirkungsgrades und ihrer Vielseitigkeit in verschiedenen Branchen eingesetzt.

Diese Zahnräder werden vor allem in Anwendungen eingesetzt, bei denen der Platz begrenzt ist, aber ein hohes Drehmoment und eine hohe Drehzahlvariabilität unerlässlich sind.

1. Automobilgetriebe: Planetengetriebe sind eine Schlüsselkomponente in Automatikgetrieben und ermöglichen nahtlose Gangwechsel, ein hohes Drehmoment bei niedrigen Drehzahlen und eine effiziente Kraftübertragung.
2. Industriemaschinen: Sie werden in Schwermaschinen eingesetzt, da sie hohe Lasten bewältigen, das Drehmoment gleichmäßig verteilen und auf engstem Raum effizient arbeiten können.
3. Luft- und Raumfahrt: Diese Zahnräder spielen eine entscheidende Rolle in Flugzeugtriebwerken und Hubschrauberrotoren und gewährleisten Zuverlässigkeit und präzise Bewegungssteuerung auch unter anspruchsvollen Bedingungen.
4. Robotik und Automatisierung: In der Robotik werden Planetengetriebe eingesetzt, um auf engstem Raum eine präzise Bewegungssteuerung, eine kompakte Bauweise und ein hohes Drehmoment zu erreichen.

Was sind die vier Elemente des Planetengetriebes?

Ein Planetengetriebe, auch bekannt alsPlanetengetriebe Das System ist ein hocheffizienter und kompakter Mechanismus, der häufig in Automobilgetrieben, Robotern und Industriemaschinen eingesetzt wird. Dieses System besteht aus vier Schlüsselelementen:

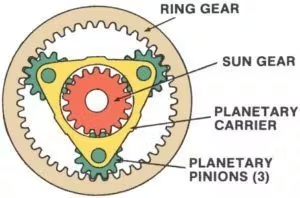
1. SonnenausrüstungDas Sonnenrad, das sich im Zentrum des Getriebes befindet, ist der primäre Antrieb bzw. Empfänger der Bewegung. Es greift direkt in die Planetenräder ein und dient häufig als Ein- oder Ausgang des Systems.

2. PlanetenräderEs handelt sich um mehrere Zahnräder, die sich um das Sonnenrad drehen. Sie sind auf einem Planetenträger montiert und kämmen sowohl mit dem Sonnenrad als auch mit dem Hohlrad. Die Planetenräder verteilen die Last gleichmäßig, wodurch das System hohe Drehmomente aufnehmen kann.

3.PlanetenträgerDieses Bauteil fixiert die Planetenräder und ermöglicht deren Rotation um das Sonnenrad. Je nach Systemkonfiguration kann der Planetenträger als Eingangs-, Ausgangs- oder stationäres Element fungieren.

4.ZahnkranzDies ist ein großes äußeres Zahnrad, das die Planetenräder umschließt. Die inneren Zähne des Hohlrads greifen in die Planetenräder ein. Wie die anderen Elemente kann auch das Hohlrad als Eingangs- oder Ausgangselement dienen oder stillstehen.

Das Zusammenspiel dieser vier Elemente ermöglicht die Flexibilität, innerhalb einer kompakten Struktur unterschiedliche Geschwindigkeitsverhältnisse und Richtungsänderungen zu erreichen.

Wie berechnet man das Übersetzungsverhältnis in einem Planetengetriebe?

Das Übersetzungsverhältnis einesPlanetengetriebe Es hängt davon ab, welche Komponenten fest, Eingangs- und Ausgangskomponenten sind. Hier ist eine Schritt-für-Schritt-Anleitung zur Berechnung des Übersetzungsverhältnisses:

1. Die Systemkonfiguration verstehen:

Bestimmen Sie, welches Element (Sonne, Planetenträger oder Ring) stationär ist.

Ermitteln Sie die Eingangs- und Ausgangskomponenten.

2. Anwendung der Grundgleichung für das Übersetzungsverhältnis: Das Übersetzungsverhältnis eines Planetengetriebes kann wie folgt berechnet werden:

GR = 1 + (R / S)

Wo:

GR = Übersetzungsverhältnis

R = Zähnezahl des Hohlrads

S = Anzahl der Zähne am Sonnenrad

Diese Gleichung gilt, wenn der Planetenträger der Abtrieb ist und entweder das Sonnenrad oder das Hohlrad stillsteht.

3. Anpassung für andere Konfigurationen:

• Wenn das Sonnenrad stillsteht, wird die Ausgangsdrehzahl des Systems durch das Übersetzungsverhältnis von Hohlrad und Planetenträger beeinflusst.
• Wenn das Hohlrad stillsteht, wird die Abtriebsdrehzahl durch das Verhältnis zwischen Sonnenrad und Planetenträger bestimmt.

4. Übersetzungsverhältnis für die Umkehrung (Ausgangs-/Eingangsdrehzahl): Bei der Berechnung der Drehzahlreduzierung (Eingangsdrehzahl höher als Ausgangsdrehzahl) ist das Verhältnis direkt. Bei der Drehzahlerhöhung (Ausgangsdrehzahl höher als Eingangsdrehzahl) wird das berechnete Verhältnis umgekehrt.

Beispielrechnung:

Angenommen, ein Zahnradsatz hat folgende Eigenschaften:

Hohlrad (R): 72 Zähne

Sonnenrad (S): 24 Zähne

Wenn der Planetenträger der Abtrieb ist und das Sonnenrad stillsteht, beträgt das Übersetzungsverhältnis:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Das bedeutet, dass die Ausgangsgeschwindigkeit viermal langsamer ist als die Eingangsgeschwindigkeit, was ein Untersetzungsverhältnis von 4:1 ergibt.

Das Verständnis dieser Prinzipien ermöglicht es Ingenieuren, effiziente und vielseitige Systeme zu entwickeln, die auf spezifische Anwendungen zugeschnitten sind.