Planetengetriebe finden als Antriebsmechanismus breite Anwendung in verschiedenen technischen Bereichen, beispielsweise in Getrieben, Kränen und Planetengetrieben. Bei Planetengetrieben können sie in vielen Fällen die Kraftübertragung von Festachsgetrieben ersetzen. Da die Kraftübertragung auf Linienkontakt beruht, kann ein längerer Eingriff zu Getriebeschäden führen. Daher ist die Simulation der Festigkeit erforderlich. Li Hongli et al. nutzten die automatische Vernetzungsmethode zur Simulation des Planetengetriebes und stellten einen linearen Zusammenhang zwischen Drehmoment und maximaler Spannung fest. Wang Yanjun et al. vernetzten das Planetengetriebe ebenfalls mithilfe der automatischen Generierungsmethode und simulierten dessen Statik und Modalanalyse. In dieser Arbeit werden hauptsächlich Tetraeder- und Hexaederelemente zur Vernetzung verwendet. Die Ergebnisse werden anschließend analysiert, um zu prüfen, ob die Festigkeitsbedingungen erfüllt sind.

1. Modellerstellung und Ergebnisanalyse

Dreidimensionale Modellierung eines Planetengetriebes

PlanetengetriebeDas Getriebe besteht hauptsächlich aus Hohlrad, Sonnenrad und Planetenrad. Die wichtigsten in dieser Arbeit gewählten Parameter sind: Zähnezahl des Hohlrads: 66, Zähnezahl des Sonnenrads: 36, Zähnezahl des Planetenrads: 15, Außendurchmesser des Hohlrads: 150 mm, Modul: 2 mm, Eingriffswinkel: 20°, Zahnbreite: 20 mm, Kopfkreishöhenkoeffizient: 1, Zahnflankenspielkoeffizient: 0,25, und es sind drei Planetenräder vorhanden.

Statische Simulationsanalyse eines Planetengetriebes

Materialeigenschaften definieren: Importieren Sie das in der UG-Software gezeichnete dreidimensionale Planetengetriebe in ANSYS und legen Sie die Materialparameter wie in Tabelle 1 unten dargestellt fest:

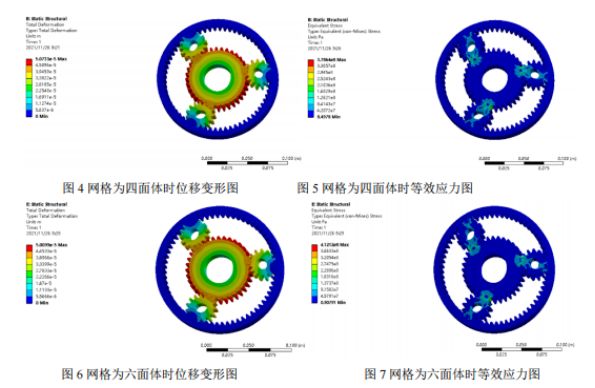
Vernetzung: Das Finite-Elemente-Netz ist in Tetraeder und Hexaeder unterteilt, die Grundgröße der Elemente beträgt 5 mm. Da diePlanetengetriebeSonnenrad und Innenzahnkranz stehen in Kontakt und greifen ineinander. Die Eingriffsfläche ist verdichtet und hat eine Maschenweite von 2 mm. Zunächst werden Tetraedergitter verwendet (siehe Abbildung 1). Insgesamt werden 105.906 Elemente und 177.893 Knoten generiert. Anschließend wird ein Hexaedergitter verwendet (siehe Abbildung 2), wodurch insgesamt 26.957 Zellen und 140.560 Knoten entstehen.

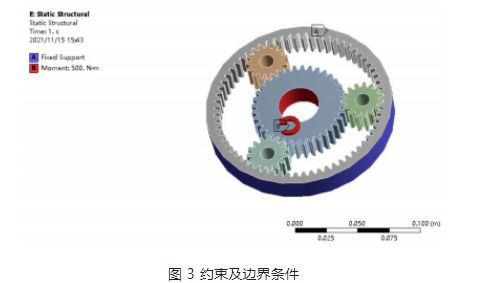
Lastaufbringung und Randbedingungen: Gemäß den Betriebseigenschaften des Planetengetriebes im Untersetzungsgetriebe ist das Sonnenrad das Antriebsrad, das Planetenrad das Abtriebsrad, und die Endkraft wird über den Planetenträger übertragen. Fixieren Sie den inneren Zahnkranz in ANSYS und legen Sie ein Drehmoment von 500 Nm auf das Sonnenrad an (siehe Abbildung 3).

Nachbearbeitung und Ergebnisanalyse: Die Verschiebungs- und Vergleichsspannungsdiagramme der statischen Analyse, ermittelt mit zwei Gitterunterteilungen, sind unten dargestellt und werden vergleichend analysiert. Aus den Verschiebungsdiagrammen der beiden Gitterarten geht hervor, dass die maximale Verschiebung an der Stelle auftritt, an der das Sonnenrad nicht mit dem Planetenrad im Eingriff ist, und die maximale Spannung am Zahnfuß. Die maximale Spannung des Tetraedergitters beträgt 378 MPa, die des Hexaedergitters 412 MPa. Da die Streckgrenze des Materials 785 MPa und der Sicherheitsfaktor 1,5 beträgt, ergibt sich eine zulässige Spannung von 523 MPa. Die maximale Spannung beider Ergebnisse liegt unterhalb der zulässigen Spannung, sodass die Festigkeitsanforderungen erfüllt sind.

2. Schlussfolgerung

Mithilfe der Finite-Elemente-Simulation des Planetengetriebes werden das Verschiebungs- und das Vergleichsspannungsdiagramm des Getriebesystems ermittelt, woraus die Maximal- und Minimalwerte sowie deren Verteilung bestimmt werden.PlanetengetriebeEin Modell kann gefunden werden. Die Stelle der maximalen Vergleichsspannung ist gleichzeitig die Stelle, an der die Zahnräder am ehesten versagen. Daher sollte diesem Bereich bei der Konstruktion oder Fertigung besondere Aufmerksamkeit gewidmet werden. Durch die Analyse des gesamten Planetengetriebesystems wird der Fehler, der durch die Analyse nur eines einzelnen Zahnrads entsteht, behoben.